线性回归--最小二乘法
对于线性回归问题,给定一个样本,其根据假设函数得到的预估结果为: \(h(x_i) = \mathbf{\theta}^T \mathbf{x_i} = y_j\) 。给出所有的样本,我们可以写成矩阵的形式即:\(X\vec{\theta} = \vec{y}\)。这种形式可以看成线性代数里的线性方程组求解问题。
如果 \(X\vec{\theta} = \vec{y}\) 方程组有解,即说明 \(\vec{y}\) 是可以用 \(X\) 的列子空间表示,即在列子空间上。但是如果方程组无解,则说明 \(\vec{y}\) 不在 \(X\) 的列空间上。所以我可以通过求得一个最优解 \(\theta\) 来解决这个方程,最优解可以使误差最小,线性代数里的最小二乘法可求得这个最优解。线性代数里的最优解,其实是求得 \(\vec{y}\) 在 \(X\) 上列空间上的投影,而投影总是离子空间最近,误差最小。下面介绍下线性代数里的投影问题。
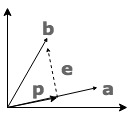
以二维空间为例,很明显,\(\vec{a}, \vec{b}\) 是不相关的。\(\vec{b}\) 是不能被 \(\vec{a}\) 表示的,但是我们可以求解一个用 \(\vec{a}\) 来表示 \(\vec{b}\) 的最优表示,这个最优表示使得误差最小(线性不相关,表示肯定是有误差的)。在这里这个最优的表示就是投影 \(\vec{p}\),误差就是 \(\vec{e}\).
投影 \(\vec{p} = \hat{x}\vec{a}\), 误差 \(\vec{e} = \vec{b} - \vec{p} = \vec{b} - \hat{x}\vec{a}\)。\(\vec{e}\) 与 \(\vec{a}\) 正交,所以有 \(\vec{a}^T \cdot \vec{e} = 0\):
\[\begin{aligned} \vec{a} ^ T \cdot \vec{e} &= 0 \\ \vec{a} ^ T \cdot (\vec{b} - \hat{x}\vec{a}) &= 0 \\ \vec{a} ^ T \vec{b} &= \hat{x} \vec{a} ^ T \vec{a} \\ \hat{x} &= \frac{\vec{a} ^ T \vec{b}} {\vec{a} ^ T \vec{a}} \end{aligned}\]所以,
\[\begin{aligned} \vec{Proj}_b &= \hat{x} \cdot \vec{a} \\ &= \vec{a} \cdot \hat{x} \\ &= \vec{a} \cdot \frac{\vec{a} ^ T \vec{b}} {\vec{a} ^ T \vec{a}} \\ &= \frac{\vec{a} \vec{a} ^ T} {\vec{a}^ T \vec{a}} \cdot \vec{b} \end{aligned}\]其中 \(P = \frac{\vec{a} \cdot \vec{a} ^ T} {\vec{a}^ T \cdot \vec{a}}\) 为投影矩阵.
对于 \(X\vec{\theta} = \vec{y}\) 而言,当方程组有解时,说明 \(\vec{y}\) 可以由 \(X\) 的列子空间表示,可以直接求出 \(\vec{\theta}\), 当无解时,也利用 \(\vec{y}\) 在 \(X\) 上的列子空间的投影来求得一个最优解 \(\hat{\vec{\theta}}\)。
\[\begin{aligned} X^T \cdot (\vec{y} - X \hat{\vec{\theta}}) &= 0 \\ X ^ T \cdot \vec{y} &= X^T X \hat{\vec{\theta}} \\ \hat{\vec{\theta}} &= (X^T X)^{-1} X ^ T \vec{y} \end{aligned}\]则 \(\hat{\vec{\theta}}\) 即是我们的最优解。些时投影为 \(Proj = X \cdot \hat{\vec{\theta}} = X \cdot (X^T X)^{-1} X ^ T \vec{y}\), 而 \(P = X \cdot (X^T X)^{-1} X ^ T\) 为投影矩阵。