线性回归(上) -- 引子
线性回归很简单呀!从这个词中可以看到两点,线性与回归。
我们先从最简单的线性说起。说起线,最简单的当然还是直线了。给出任意两点可以画出一条直线(当然我说的是欧氏几何)。
那问一个简单的问题,给你三个点不共线,你还能画出一条过这三个点的直线吗?答案是否定的,因为已经说了是不共线的三点?但是如果非要画一条直线怎么办?给出一个托马斯的问题,假设要在美丽的多多岛上的三个城市修条铁路,这三个站不共线,但是小火车又只能开直线,那么这条笔直的铁路要怎么修那?
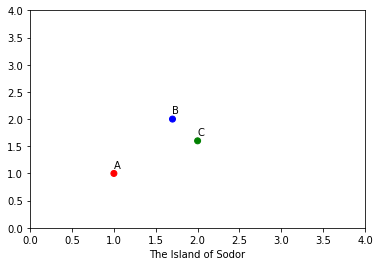
最优的方案是修一条铁路离三个站点的总距离是最小的。我们怎么找到出条直线那?下面我们尝试用线性代数中的投影矩阵知识解决这个问题。
投影问题
怎么用这三个点形成的向量表示一条直线,使得这条直线离这三个点的总距离最近。下面引用线性代数的投影问题。
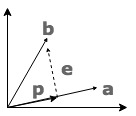
二维向量空间中,\(\vec{a}, \vec{b}\) 是线性不相关的,很显然两个向量之间是无法相互表示的。如果非要用 \(\vec{a}\) 来表示 \(\vec{b}\) ,我们应该怎么表示那?假设我们找出向量 \(\vec{p}\) 表示 \(\vec{b}\),这种表示肯定是有误差的。这个误差怎么计算,可以算两个向量的 cosine 值表示两个向量的差异。假设误差向量为 \(\vec{e}\),那么当 \(\vec{b}\) 与 \(\vec{b}\)垂直正交时的误差(距离)最小喽。所以看出投影问题也是解决怎么找到最小距离的问题。
下面就投影问题例下公式, 投影 \(\vec{p} = \hat{x}\vec{a}\), 误差 \(\vec{e} = \vec{b} - \vec{p} = \vec{b} - \hat{x}\vec{a}\)。\(\vec{e}\) 与 \(\vec{a}\) 正交,所以有 \(\vec{a}^T \cdot \vec{e} = 0\):
\[\begin{aligned} \vec{a} ^ T \cdot \vec{e} &= 0 \\ \vec{a} ^ T \cdot (\vec{b} - \hat{x}\vec{a}) &= 0 \\ \vec{a} ^ T \vec{b} &= \hat{x} \vec{a} ^ T \vec{a} \\ \hat{x} &= \frac{\vec{a} ^ T \vec{b}} {\vec{a} ^ T \vec{a}} \end{aligned}\]所以,
\[\begin{aligned} \vec{Proj}_b &= \hat{x} \cdot \vec{a} \\ &= \vec{a} \cdot \hat{x} \\ &= \vec{a} \cdot \frac{\vec{a} ^ T \vec{b}} {\vec{a} ^ T \vec{a}} \\ &= \frac{\vec{a} \vec{a} ^ T} {\vec{a}^ T \vec{a}} \cdot \vec{b} \end{aligned}\]其中 \(P = \frac{\vec{a} \cdot \vec{a} ^ T} {\vec{a}^ T \cdot \vec{a}}\) 为投影矩阵。 \(\hat{x}\), x hat 一般表示是一个估计值。
对于多多岛三个站点的问题,我们也想找到一个投影直线,使得这个投影直线离三个站点的距离都是最短的,怎么找那?假设三个站点对应的向量分别为 \(\vec{a}^T = (1, 2)\), \(\vec{b}^T = (2, 1.7)\), \(\vec{c}^T = (3.5, 3)\)。
对于一维空间一个向量求其投影问题按上式很简单,如果给一组向量怎么求其投影那?假设一组向量组成的矩阵为 \(X\) 想要表示 \(\vec{y}\),怎么求出这表示?即求出 \(X\vec{\theta} = \vec{y}\), 其中 \(\vec{\theta} = (\theta_0, \theta_1, ...)^T\)。 那么这个问题到回到线性代数最基础知识点了,即 \(X\vec{\theta} = \vec{y}\) 有解吗? 如果有解可以毫无误差的直接表示 \(\vec{y}\) 了,在二维上就是可以直接画出这条直线出来。如果无解那?那就是不能直接有 \(X\) 的列子空间来表示 \(\vec{y}\) 了, 在二维上就是画不出直线了。
如果不能直接表示那么我们可以找一个近似的表示吧,使得表示的误差最小。假设用 \(X\vec{\hat{\theta}}\) 表示 \(\vec{y}\), 误差向量为 \(X\vec{\hat{\theta}} - \vec{y}\)。当误差向量与 \(X\) 的列子空间正交(当然也与 \(X\) 正交)时误差最小,所以有 \(X^T(X\vec{\hat{\theta}} - \vec{y}) = \vec{0}\), 下面我就来求出 \(\vec{\hat{\theta}}\) .
注: \(\vec{a}\) 与 \(\vec{b}\) 正交,则 \(\vec{a}^T \vec{b} = \vec{b}^T \vec{a} = \vec{0}\)
\[\begin{aligned} X^T(X\vec{\hat{\theta}} - \vec{y}) &= \vec{0} \\ X^TX\vec{\hat{\theta}} &= X^T\vec{y} \\ \hat{\vec{\theta}} &= (X^TX)^{-1}X^T\vec{y} \end{aligned}\]\(\hat{\vec{\theta}}\) 即是我们的误差表示的最优解。些时投影为 \(Proj = X \cdot \hat{\vec{\theta}} = X \cdot (X^T X)^{-1} X ^ T \vec{y}\), 而 \(P = X \cdot (X^T X)^{-1} X ^ T\) 为投影矩阵。
多多岛的解决方案
下面用线性代数的最优解来解决多多岛的问题。针对这个最优问题也可能有多种方案。如规定这条铁路要城市A, B 的下边,C 的上边,那可能画出的就是 Line 1, 如果规定铁路要在城市 B 的下面,A, C 的上面,那可能画出的就是 Line 2,如果全部三点的上面下面也是可能的。(铁路不能直接建上城市上,因为扰民…🙃)
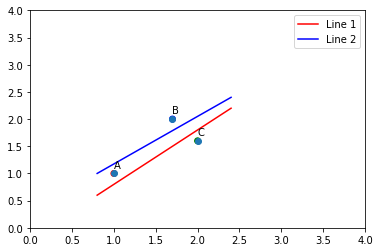
我们来分个类,在线上边的标记为 1,在线下边的标记为 -1。 现在解决 A, B 在线的上边、 C 在线下面的最佳直线的问题。那么这三个点的分类是 \([1; 1; -1]\)。
我们假设这条直线为: \(h(x) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 = \vec{\theta^T} \vec{x}\), 其中 \(x_0 = 1\)。 (我们平面中见的最多的直线表示还是 \(ax + by + c = 0\)).
根据上面线性代数的推导,我们可以求出最优解 \(\hat{\vec{\theta}} = (X^TX)^{-1}X^T\vec{y}\). 其中 X 就是\((x_0, x_1, x_2)\) 组成的矩阵,\(y = [1; 1; -1]\) 是三个分类的标识(Label).
\[X = \begin{bmatrix} 1 & 1 & 1\\ 1 & 1.7 & 2\\ 1 & 2 & 1.6 \end{bmatrix} y = \begin{bmatrix} 1 \\ 1 \\ -1 \end{bmatrix}\]用 Matlab 解决这个问题, 在 Matlab 中输入下面指令算出 \(\theta\)
X = [1 1 1; 1 1.7 2; 1 2 1.6]
y = [1;1;-1]
thetas = inv(X.'*X)*X.'*y
最后得出:
\[y = \begin{bmatrix} 2.0345 \\ -3.4483 \\ 2.4138 \end{bmatrix}\]所以我们的直线就是: \(-3.4483 x_1 + 2.4138 x_2 + 2.0345 = 0\). 下面我们用 python 我解决这个问题,并且用 matplotlib 画出这条直线。顺便说一下求 \(\theta\) 的方法是最小二乘法(Least Squares Method,简记为LSE), 而 \(\theta\) 称为系数(weights).
代码实现
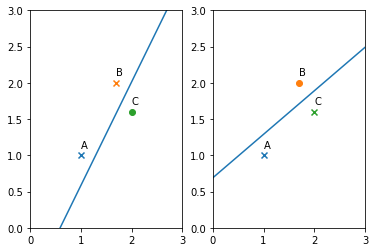
三个城市,通过两组不的标签 \(yLabels1 = [1, 1, -1]\) 和 \(yLabels2 = [1, -1, 1]\)来画出两条最优的直线。
import numpy as np
def get_LSE_weights(yLabels):
''' 最小二乘法 '''
y = np.mat(yLabels).T
X = np.mat([[1, 1, 1], [1, 1.7, 2], [1, 2, 1.6]])
return (X.T * X).I * X.T * y
def plotLine(ax, weights):
x_1 = np.arange(0, 3.5, 0.1)
x_2 = (-weights[0] - weights[1] * x_1) / weights[2] # x2 = (-w0 - w1*x1)/w2
ax.plot(x_1, np.squeeze(np.asarray(x_2)))
def plotIsland(ax, y):
t = ['A', 'B', 'C']
ax.set_xlim([0, 3])
ax.set_ylim([0, 3])
x1 = [1, 1.7, 2]
x2 = [1, 2, 1.6]
for i in range(3):
m = 'x'
if y[i] == -1:
m = 'o'
ax.scatter(x1[i], x2[i], marker=m)
ax.annotate(t[i], (x1[i], x2[i] + 0.1))
fig, (ax1, ax2) = plt.subplots(1, 2)
yLabels1 = [1, 1, -1]
plotIsland(ax1, yLabels1)
yLabels2 = [1, -1, 1]
plotIsland(ax2, yLabels2)
weights = get_LSE_weights(yLabels1)
plotLine(ax1, weights)
weights = get_LSE_weights(yLabels2)
plotLine(ax2, weights)
plt.show()
到目前为止,多多岛的铁路线总找到了。我们找到这条线的过程就是回归。所以到目前为止我们『线性回归』总算过了初级阶段。回归英文单词 Regression 的释义是 an abnormal state in which development has stopped prematurely 即是一个不能再进化的最优解状态。
在下一篇,我们将介绍真正的线性回归。从机器学习的 hypothesis, cost function 出发,利用梯度算法来介绍线性回归。